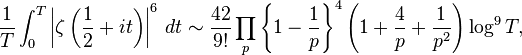My wife's cousin, George Smith, put a number of interesting facts on his facebook page today regarding 10.10.10 As George points out, when you look at 101010 as the binary representation of decimal 42, then it gets to be a really interesting day:
As Wikipedia also points out about 42 decimal:
- Given 27 same-size cubes whose nominal values progress from 1 to 27, a 3×3×3 magic cube can be constructed such that every row, column, and corridor, and every diagonal passing through the center, comprises 3 cubes whose sum of values is 42.
- Forty-two is a pronic number and an abundant number; its prime factorization 2 · 3 · 7 makes it the second sphenic number and also the second of the form { 2 · 3 · r }. As with all sphenic numbers of this form, the aliquot sum is abundant by 12. 42 is also the second sphenic number to be bracketed by twin primes; 30 is also a pronic number and also rests between two primes. 42 has a 14 member aliquot sequence 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1, 0 and is itself part of the aliquot sequence commencing with the first sphenic number 30. Further, 42 is the 10th member of the 3-aliquot tree.
- It is a Catalan number. Consequently; 42 is the number of noncrossing partitions of a set of five elements, the number of triangulations of a heptagon, the number of rooted ordered binary trees with six leaves, the number of ways in which five pairs of nested parentheses can be arranged, etc.
- Since the greatest prime factor of 422 + 1 = 1765 is 353 and thus more than 42 twice, 42 is a Størmer number.
- The eight digits of pi beginning from 242,422 places after the decimal point are 42424242.
- 42 is the expected number of throws of a (single) fair die until two sixes show up successively (for the first time).
In technology
- Magic numbers used by programmers:
- The glyph, or character, corresponding to the number 42 in the ASCII character set, is *, the asterisk, commonly known as the wildcard character. For example, when used in a Unix command such as "rm -fr /*", * means "everything".
- In the TIFF image file format, the second 16-bit word of every file is 42, which is used together with the first word to indicate byte order.
- In the reiser4 file system, 42 is the inode number of the root directory.